Aufgabe 22 (K)
- Kubik-Rubik
- Administrator
- Beiträge: 267
- Registriert: Di 21. Okt 2008, 19:55
- Wohnort: Kehl / Karlsruhe
Aufgabe 22 (K)
Hier kommen Fragen und Antworten zur 22. Aufgabe rein!
Registrierung nur noch mit E-Mail Adresse der Universität Karlsruhe möglich.
Mehr Informationen: Registrierung nur noch mit E-Mail Adresse der Universität
Notation für Übungsblätter - FACH[x]#y (Blatt x - Aufgabe y für FACH)
Mehr Informationen: Registrierung nur noch mit E-Mail Adresse der Universität
Notation für Übungsblätter - FACH[x]#y (Blatt x - Aufgabe y für FACH)
-
Thomas
- Administrator
- Beiträge: 383
- Registriert: Do 23. Okt 2008, 20:16
- Wohnort: Karlsruhe
- Kontaktdaten:
Re: Aufgabe 22 (K)
ich post mal meine lösungen zum vergleichen:
a) konvergiert für x element [-1,1); KR=1
b) konvergiert für x element (-1,1); KR=1
c) konvergiert für x element R; KR= + unendlich
d) konvergiert für x element) ; KR =
; KR = 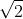
was habt ihr so raus?
a) konvergiert für x element [-1,1); KR=1
b) konvergiert für x element (-1,1); KR=1
c) konvergiert für x element R; KR= + unendlich
d) konvergiert für x element
was habt ihr so raus?
-
Scotty_doesn't_know
- Beiträge: 9
- Registriert: So 9. Nov 2008, 12:29
Re: Aufgabe 22 (K)
a) konvergiert für x element [-1,1]; KR=1 für x=1 konvergiert die Reihe doch auch oder ?!Thomas hat geschrieben:ich post mal meine lösungen zum vergleichen:
a) konvergiert für x element [-1,1); KR=1
b) konvergiert für x element (-1,1); KR=1
c) konvergiert für x element R; KR= + unendlich
d) konvergiert für x element; KR =
was habt ihr so raus?
b) konvergiert für x element (-1,1); KR=1 hab ich auch!
c)+d) ist noch in Arbeit...
-
Thomas
- Administrator
- Beiträge: 383
- Registriert: Do 23. Okt 2008, 20:16
- Wohnort: Karlsruhe
- Kontaktdaten:
Re: Aufgabe 22 (K)
für 1 hab ich 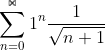 1^n ist immer 1 also bleibt der wurzelterm. den hab ich nach unten abgeschätzt, also >= 1/n und da
1^n ist immer 1 also bleibt der wurzelterm. den hab ich nach unten abgeschätzt, also >= 1/n und da 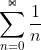 divergiert müsste dann auch
divergiert müsste dann auch 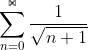 divergieren oder?
divergieren oder?
Re: Aufgabe 22 (K)
ich habe:
a) [-1,1)
b) (-1,1)
c) [-0.5*e, 0.5*e]
d) 0
a) [-1,1)
b) (-1,1)
c) [-0.5*e, 0.5*e]
d) 0
-
Christian S.
- Beiträge: 225
- Registriert: Sa 25. Okt 2008, 12:48
Re: Aufgabe 22 (K)
Habe ich bis auf die d) auch so. Wie kommst du zu dem Ergebnis? Ich nehme mal an du hast eine Lückenreihe gebildet. Mir ist aber nicht ganz klar, was ich dann beim Wurzelkriterium in die Wurzel und was ich als 1/x (Wurzel) habe.Chrisor hat geschrieben:ich habe:
a) [-1,1)
b) (-1,1)
c) [-0.5*e, 0.5*e]
d) 0
-
Thomas
- Administrator
- Beiträge: 383
- Registriert: Do 23. Okt 2008, 20:16
- Wohnort: Karlsruhe
- Kontaktdaten:
Re: Aufgabe 22 (K)
also ich hab die c) so gemacht. bei der d is mir glaub ich ein fehler unterlaufen
PRIME_BBCODE_SPOILER_SHOW PRIME_BBCODE_SPOILER: auf Anzeigen klicken
c)
^{n}* n!)
dann:
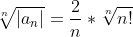
für n gegen unendlich würde dann gelten : 0*1 = 0 und draraus folgt KR = +unendlich
wie hast dus gelöst chrisor?
dann:
für n gegen unendlich würde dann gelten : 0*1 = 0 und draraus folgt KR = +unendlich
wie hast dus gelöst chrisor?
-
Christian S.
- Beiträge: 225
- Registriert: Sa 25. Okt 2008, 12:48
Re: Aufgabe 22 (K)
Das Problem ist aber, dass die n. Wurzel von n! gegen unendlich und nicht gegen 1 gehtThomas hat geschrieben:also ich hab die c) so gemacht. bei der d is mir glaub ich ein fehler unterlaufenPRIME_BBCODE_SPOILER_SHOW PRIME_BBCODE_SPOILER: auf Anzeigen klickenc)
dann:
für n gegen unendlich würde dann gelten : 0*1 = 0 und draraus folgt KR = +unendlich
wie hast dus gelöst chrisor?
Ich habe es per diesem L = an / an+1 gemacht.
-
Thomas
- Administrator
- Beiträge: 383
- Registriert: Do 23. Okt 2008, 20:16
- Wohnort: Karlsruhe
- Kontaktdaten:
Re: Aufgabe 22 (K)
ah stimmt war ja n-te wurzel n dass gegen 1 geht sry.
für die d) hab ich mittlerweile:
zur c) nochma:
wenn ich da dann aber |an/an+1| mache bekomm ich doch am schluss}) da fehlt ja dann aber das ^n oder hab ich nochma was falsch gemacht?
da fehlt ja dann aber das ^n oder hab ich nochma was falsch gemacht?
für die d) hab ich mittlerweile:
PRIME_BBCODE_SPOILER_SHOW PRIME_BBCODE_SPOILER: auf Anzeigen klicken
für k = n²
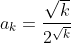
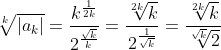
für k gegen unendlich geht sowohl zähler als auch nenner gegen 1
sonst ak = 0
damit wäre lim sup 1
was meint ihr?
für k gegen unendlich geht sowohl zähler als auch nenner gegen 1
sonst ak = 0
damit wäre lim sup 1
was meint ihr?
wenn ich da dann aber |an/an+1| mache bekomm ich doch am schluss
Re: Aufgabe 22 (K)
hab da am ende wenn ich das "L" mache 0,5 * (n+1/n)^n....Thomas hat geschrieben: zur c) nochma:
wenn ich da dann aber |an/an+1| mache bekomm ich doch am schlussda fehlt ja dann aber das ^n oder hab ich nochma was falsch gemacht?
das wäre dann für n gegen unendlich 0,5 e oder?