4. Übungsblatt - Abgabe 20. November
Re: 4. Übungsblatt - Abgabe 20. November
sorry nich gesehen...
aber musst du nicht nach unten abschätzen?
ich mein (2/3)^n geht gegen null und ist nur 2/3 für n=1
es geht doch darum welchen wert das annimmt wenn n immer größer wird...
aber musst du nicht nach unten abschätzen?
ich mein (2/3)^n geht gegen null und ist nur 2/3 für n=1
es geht doch darum welchen wert das annimmt wenn n immer größer wird...
Re: 4. Übungsblatt - Abgabe 20. November
Hi!
Ich versuche es auch zu loesen.
Bei 14. a) = 1/2 und 14. d) = e^(3/2) bin ich mir auch fasst sicher. Bei den 2 ubrigen, c) und b) hab ich Probleme. Aber jedenfalls denke ich, dass es nicht so ganz leicht geht, und auch wenn es so waere dann haette man es irgendwie rational beweisen muessen. Viel Gluck!
p.s. Wie loest ihr die 16K? Ahnlich dem Muster aus der letzten Ubung?
Ich versuche es auch zu loesen.
Bei 14. a) = 1/2 und 14. d) = e^(3/2) bin ich mir auch fasst sicher. Bei den 2 ubrigen, c) und b) hab ich Probleme. Aber jedenfalls denke ich, dass es nicht so ganz leicht geht, und auch wenn es so waere dann haette man es irgendwie rational beweisen muessen. Viel Gluck!
p.s. Wie loest ihr die 16K? Ahnlich dem Muster aus der letzten Ubung?
Zuletzt geändert von P178ULL am Di 18. Nov 2008, 17:41, insgesamt 1-mal geändert.
Re: 4. Übungsblatt - Abgabe 20. November
So kann man leider nicht argumentieren... angenommen du hast b(n) := (1/2)^(1/n) und a(n) := (b(n))^n. Jetzt hat man b(n) < 1 aber a(n) = ((1/2)^(1/n))^n = (1/2)^(1/n * n) = 1/2.Christian S. hat geschrieben:Doch, darfst du. Denn egal welchen 0 =< Wert <1 du nimmst, er geht hoch irgendwas immer gegen 0. Bei (1+1/n) ist dies nicht der Fall, denn 1+1/n ist >1. Schau einfach mal im Skript bei 2.7 vom 4.11. nach, da haben wir für genau diesen Folgenteil gezeigt, dass er =< sqrt(2) / sqrt(n-1) ist. Und das ist kleiner 1 für n >= 4. Somit hast du 0 =< b(n) < 1.
=> b(n)^n ----> 0 für n -> unendlich.
btw... vielleicht sollten wir mal für b) und c) nen neuen Thread aufmachen. Wird langsam etwas unübersichtlich.
-
Christian S.
- Beiträge: 225
- Registriert: Sa 25. Okt 2008, 12:48
Re: 4. Übungsblatt - Abgabe 20. November
Da gebe ich dir recht. Mit meinem "irgendwas" meinte ich auch "irgendwas" aus |N. Und innerhalb der Klammer hast du ja keine weitere Potenz. Von demher sehe ich nicht, wieso das argumentativ und logisch nicht richtig sein sollte. Denn wenn ich zeige, dass die Klammer größer gleich Null und echt kleiner 1 ist, weiß ich doch, dass die Klammer hoch n für n ---> unendlich gegen 0 geht. Wie gesagt, ich habe wie in Beispiel 2.7 gezeigt, dass der Inhalt der Klammer echt kleiner 1 ist. Ich hoffe ich drehe mich hier nicht im Kreis und man kann meinem Post hier zumindest meine Kernaussage abgewinnenelTybbq hat geschrieben:So kann man leider nicht argumentieren... angenommen du hast b(n) := (1/2)^(1/n) und a(n) := (b(n))^n. Jetzt hat man b(n) < 1 aber a(n) = ((1/2)^(1/n))^n = (1/2)^(1/n * n) = 1/2.Christian S. hat geschrieben:Doch, darfst du. Denn egal welchen 0 =< Wert <1 du nimmst, er geht hoch irgendwas immer gegen 0. Bei (1+1/n) ist dies nicht der Fall, denn 1+1/n ist >1. Schau einfach mal im Skript bei 2.7 vom 4.11. nach, da haben wir für genau diesen Folgenteil gezeigt, dass er =< sqrt(2) / sqrt(n-1) ist. Und das ist kleiner 1 für n >= 4. Somit hast du 0 =< b(n) < 1.
=> b(n)^n ----> 0 für n -> unendlich.
btw... vielleicht sollten wir mal für b) und c) nen neuen Thread aufmachen. Wird langsam etwas unübersichtlich.
Viele Grüße,
Christian
Re: 4. Übungsblatt - Abgabe 20. November
mh, hier nochma meine version von a und c, wenn hirnfick sagen 
Du hast keine ausreichende Berechtigung, um die Dateianhänge dieses Beitrags anzusehen.
I HAS FREE CANDYZ
-
localhorst
- Beiträge: 28
- Registriert: Sa 8. Nov 2008, 19:39
- Wohnort: hadiko
Re: 4. Übungsblatt - Abgabe 20. November
Bei der b) hab ich folgendermaßen argumentiert:
2^n >= n (n € N)
gilt, kam in vorlesung/übung/tut.. für n>=2 gilt
2^n > n (n € N)
also
2 > n-rt(n)
außerdem gilt
n-rt(n) >=1
Somit ist
0 <= n-rt(n) -1 < 1
und daraus die potenz geht gegen null.. letzendlich weil n-rt(n) auch immer kleiner wird, nicht größer..
zu c)
bei sämtlichen abschätzungen muss man ja noch beweisen dass sie monoton fallend ist, da finde ich die direkten beweise netter..
2^n >= n (n € N)
gilt, kam in vorlesung/übung/tut.. für n>=2 gilt
2^n > n (n € N)
also
2 > n-rt(n)
außerdem gilt
n-rt(n) >=1
Somit ist
0 <= n-rt(n) -1 < 1
und daraus die potenz geht gegen null.. letzendlich weil n-rt(n) auch immer kleiner wird, nicht größer..
zu c)
bei sämtlichen abschätzungen muss man ja noch beweisen dass sie monoton fallend ist, da finde ich die direkten beweise netter..
Zuletzt geändert von localhorst am Di 18. Nov 2008, 22:15, insgesamt 1-mal geändert.
-
Chris
- Beiträge: 109
- Registriert: Mo 3. Nov 2008, 20:31
- Wohnort: ca. 5 min zum HSaF ;) also Karlsruhe
- Kontaktdaten:
Re: 4. Übungsblatt - Abgabe 20. November
und hier noch die 16 a)
für n gerade:
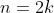
^{2k-1}}{2k} \right)^{2k})
^{2k})
^{-2k})
^{2k} \right)^{-1})
^{2k-1} * \left(\frac{2k}{2k-1} \right)\right)^{-1})
Für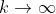
der 1. Ausdruck:
gegen
der 2. Ausdruck:
gegen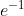
Am Ende noch ordentlich hinschreiben mit limsup und liminf und ferdisch
danach für n ungerade:
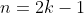
^{2k-2}}{2k-1} \right)^{2k-1})
^{2k-1})
geht das ganze wie bei n gerade gegen
für n gerade:
Für
der 1. Ausdruck:
gegen
der 2. Ausdruck:
gegen
Am Ende noch ordentlich hinschreiben mit limsup und liminf und ferdisch
danach für n ungerade:
geht das ganze wie bei n gerade gegen
Re: 4. Übungsblatt - Abgabe 20. November
Also es ist klar, dass x^k für 0 <= x < 1 gegen 0 geht. Da ist das x aber fest. Du behauptest das lässt sich auf Folgen übertragen also (b(n))^n ------> 0 für 0 <= b(n) < 1. Hätte ich eigentlich auch gedacht aber ich hab dir ja ein Beispiel gezeigt, bei dem es nicht stimmt, nämlich b(n) := (1/2)^(1/n). Also kann die Behauptung nicht stimmen, was kacke is, weil ich auch keine Ahnung hab wie man die b) sonst lösen soll -_-Christian S. hat geschrieben: Da gebe ich dir recht. Mit meinem "irgendwas" meinte ich auch "irgendwas" aus |N. Und innerhalb der Klammer hast du ja keine weitere Potenz. Von demher sehe ich nicht, wieso das argumentativ und logisch nicht richtig sein sollte. Denn wenn ich zeige, dass die Klammer größer gleich Null und echt kleiner 1 ist, weiß ich doch, dass die Klammer hoch n für n ---> unendlich gegen 0 geht. Wie gesagt, ich habe wie in Beispiel 2.7 gezeigt, dass der Inhalt der Klammer echt kleiner 1 ist. Ich hoffe ich drehe mich hier nicht im Kreis und man kann meinem Post hier zumindest meine Kernaussage abgewinnen.
Viele Grüße,
Christian
-
Christian S.
- Beiträge: 225
- Registriert: Sa 25. Okt 2008, 12:48
Re: 4. Übungsblatt - Abgabe 20. November
Tut mir leid, wenn das falsch rüber kam - zwar habe ich bei meiner Lösung nicht deine Einwände bedacht, aber nach dem, was wir in der Vorlesung gemacht haben, ist es für diesen speziellen Fall korrekt, wenn mich oder den Herrn Herzog nicht alles täuschtelTybbq hat geschrieben:Also es ist klar, dass x^k für 0 <= x < 1 gegen 0 geht. Da ist das x aber fest. Du behauptest das lässt sich auf Folgen übertragen also (b(n))^n ------> 0 für 0 <= b(n) < 1. Hätte ich eigentlich auch gedacht aber ich hab dir ja ein Beispiel gezeigt, bei dem es nicht stimmt, nämlich b(n) := (1/2)^(1/n). Also kann die Behauptung nicht stimmen, was kacke is, weil ich auch keine Ahnung hab wie man die b) sonst lösen soll -_-Christian S. hat geschrieben: Da gebe ich dir recht. Mit meinem "irgendwas" meinte ich auch "irgendwas" aus |N. Und innerhalb der Klammer hast du ja keine weitere Potenz. Von demher sehe ich nicht, wieso das argumentativ und logisch nicht richtig sein sollte. Denn wenn ich zeige, dass die Klammer größer gleich Null und echt kleiner 1 ist, weiß ich doch, dass die Klammer hoch n für n ---> unendlich gegen 0 geht. Wie gesagt, ich habe wie in Beispiel 2.7 gezeigt, dass der Inhalt der Klammer echt kleiner 1 ist. Ich hoffe ich drehe mich hier nicht im Kreis und man kann meinem Post hier zumindest meine Kernaussage abgewinnen.
Viele Grüße,
Christian
Re: 4. Übungsblatt - Abgabe 20. November
Ich glaube inzwischen, wir müssen die Folge mit einer anderen einschließen, die ebenfalls gegen Null gehen.
Die Argumentation mit Folge hoch n geht gegen Null funktioniert nicht ohne weiteres, man beachte das Beispiel aus der Übung: (1-1/n)^n geht gegen 1/e.
mfG
Markus
Die Argumentation mit Folge hoch n geht gegen Null funktioniert nicht ohne weiteres, man beachte das Beispiel aus der Übung: (1-1/n)^n geht gegen 1/e.
mfG
Markus